
סדרות
בכל נושא הסדרות מקובלים מספר סימונים:
a1 הוא האיבר הראשון בסידרה
an הוא האיבר ה n בסידרה
Sn הוא סכום n האיברים הראשונים בסידרה
סידרה חשבונית
סידרה חשבונית היא סידרה שבין איבריה יש הפרש קבוע.
דוגמה א': הסידרה ...1,3,5,7,9 היא סידרה חשבונית שההפרש בין איבריה הוא 2.
הסימון המקובל להפרש הוא d.
כך שלגבי הסידרה שניתנה בדוגמה א' אפשר להגיד:
a1=1
a5=9
d=2
הנוסחה למציאת האיבר ה n בסידרה חשבונית: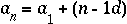

(למה צריך נוסחה בשביל האיבר ה n?)
הנוסחה למציאת סכום האיברים בסידרה חשבונית:!["nth"S = n/2[2"1st"a + (n-1)d]](sd_hsh_s.png)

סידרה הנדסית
סידרה הנדסית היא סידרה שבין איבריה יש מנה קבועה.
דוגמה ב': הסידרה ...3,12,48,192 היא סידרה הנדסית שהמנה בין איבריה היא 4 (12=3 . 4, 48=12 . 4).
הסימון המקובל למנה הוא q.
כך שלגבי הסידרה שניתנה בדוגמה ב' אפשר להגיד:
a1=3
a4=192
q=4
הנוסחה למציאת האיבר ה n בסידרה הנדסית: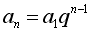

הנוסחה לחישוב סכום איברי סדרה הנדסית: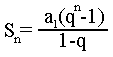

טור אינסופי מתכנס
טור אינסופי מתכנס הוא למעשה סידרה שבה
המשמעות של סידרה כזו היא קודם כל שככל שמתקדמים באיברי הסדרה, האיברים קטנים. ושנית, שסכום איברי הסדרה לעולם לא יגיע ל 1.
(למה קוראים לזה "טור" ולא "סידרה"?)
הנוסחה לחישוב סכום איברים בטור אינסופי מתכנס: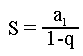

(למה זו הנוסחה?)
סדרות מעורבות
למה צריך נוסחה למציאת האיבר ה n
הסיבה הראשונה היא שאם יתנו לנו את הסידרה החביבה מדוגמה א' (...1,3,5,7,9) ואז יבקשו לדעת מהו האיבר ה37548, יקח לנו הרבה פחות זמן להשתמש בנוסחה מאשר לחשב את הזוועה הזו. הסיבה השניה היא שיבקשו את זה בבגרות, אז כדאי לדעת את זה לפני המבחן עצמו.
למה קוראים לזה "טור" ולא "סידרה"?
כי מתימטיקאים חייבים לסבך הכל. זה יצר בלתי נשלט.
מאיפה הגיעה הנוסחה לסכום טור אינסופי מתכנס
הנוסחה הגיעה מן הנוסחה המקורית לסכום סידרה הנדסית:
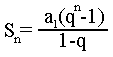
אם ניקח בחשבון שn הוא אינסוף (או שואף לאינסוף - תנאי לסדרה אינסופית), וq הוא מספר בין 1 ל -1 (תנאי לסדרה מתכנסת), נראה שהביטוי qnהוא שבר שמוכפל בעצמו המון פעמים, וכמו כל שבר במצב הזה, גם הוא קטן עם כל הכפלה, וכך יותר ויותר שואף לאפס. מאחר והסידרה היא אינסופית, הוא מגיע למצב שהוא שואף לאפס כל כך חזק שההבדל בינו לבין אפס זניח. וכך מתקבל לנו במונה: (a1 . (-1.
אותו (-1) יכול לרדת למכנה (הפיכת הסימן של המונה והסימן של המכנה לא ישנו את הסימן של השבר), ובכך יהפוך את ה1-q ל q-1. וכך הגענו לנוסחה לסכום טור אינסופי.
a1 הוא האיבר הראשון בסידרה
an הוא האיבר ה n בסידרה
Sn הוא סכום n האיברים הראשונים בסידרה
סידרה חשבונית
סידרה חשבונית היא סידרה שבין איבריה יש הפרש קבוע.
דוגמה א': הסידרה ...1,3,5,7,9 היא סידרה חשבונית שההפרש בין איבריה הוא 2.
הסימון המקובל להפרש הוא d.
כך שלגבי הסידרה שניתנה בדוגמה א' אפשר להגיד:
a1=1
a5=9
d=2
הנוסחה למציאת האיבר ה n בסידרה חשבונית:
(למה צריך נוסחה בשביל האיבר ה n?)
הנוסחה למציאת סכום האיברים בסידרה חשבונית:
סידרה הנדסית
סידרה הנדסית היא סידרה שבין איבריה יש מנה קבועה.
דוגמה ב': הסידרה ...3,12,48,192 היא סידרה הנדסית שהמנה בין איבריה היא 4 (12=3 . 4, 48=12 . 4).
הסימון המקובל למנה הוא q.
כך שלגבי הסידרה שניתנה בדוגמה ב' אפשר להגיד:
a1=3
a4=192
q=4
הנוסחה למציאת האיבר ה n בסידרה הנדסית:
הנוסחה לחישוב סכום איברי סדרה הנדסית:
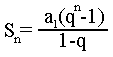
טור אינסופי מתכנס
טור אינסופי מתכנס הוא למעשה סידרה שבה
-1< q <1
ושיש בה אינסוף איברים.המשמעות של סידרה כזו היא קודם כל שככל שמתקדמים באיברי הסדרה, האיברים קטנים. ושנית, שסכום איברי הסדרה לעולם לא יגיע ל 1.
(למה קוראים לזה "טור" ולא "סידרה"?)
הנוסחה לחישוב סכום איברים בטור אינסופי מתכנס:
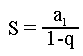
(למה זו הנוסחה?)
סדרות מעורבות
למה צריך נוסחה למציאת האיבר ה n
הסיבה הראשונה היא שאם יתנו לנו את הסידרה החביבה מדוגמה א' (...1,3,5,7,9) ואז יבקשו לדעת מהו האיבר ה37548, יקח לנו הרבה פחות זמן להשתמש בנוסחה מאשר לחשב את הזוועה הזו. הסיבה השניה היא שיבקשו את זה בבגרות, אז כדאי לדעת את זה לפני המבחן עצמו.
למה קוראים לזה "טור" ולא "סידרה"?
כי מתימטיקאים חייבים לסבך הכל. זה יצר בלתי נשלט.
מאיפה הגיעה הנוסחה לסכום טור אינסופי מתכנס
הנוסחה הגיעה מן הנוסחה המקורית לסכום סידרה הנדסית:
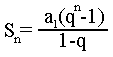
אם ניקח בחשבון שn הוא אינסוף (או שואף לאינסוף - תנאי לסדרה אינסופית), וq הוא מספר בין 1 ל -1 (תנאי לסדרה מתכנסת), נראה שהביטוי qnהוא שבר שמוכפל בעצמו המון פעמים, וכמו כל שבר במצב הזה, גם הוא קטן עם כל הכפלה, וכך יותר ויותר שואף לאפס. מאחר והסידרה היא אינסופית, הוא מגיע למצב שהוא שואף לאפס כל כך חזק שההבדל בינו לבין אפס זניח. וכך מתקבל לנו במונה: (a1 . (-1.
אותו (-1) יכול לרדת למכנה (הפיכת הסימן של המונה והסימן של המכנה לא ישנו את הסימן של השבר), ובכך יהפוך את ה1-q ל q-1. וכך הגענו לנוסחה לסכום טור אינסופי.